


Chapitre 3 : Les modèles
de vision
La modélisation des phénomènes régissant notre
vision est un domaine capital en imagerie numérique. En effet, les
temps de calcul en synthèse d'images sont très longs. Il
serait alors utile d'avoir un outil permettant de ne calculer que ce que
l'oeil est capable de voir.
Les études sur la qualité des images ont tout autant
besoin de ces modèles. Comment savoir si un résultat est
pertinent si l'algorithme d'analyse ne prend pas en compte les mécanismes
du système visuel humain ?
A partir de deux images (dont l'une pourrait être la référence,
par exemple), on applique le modèle. On obtient ainsi les deux images
telles que les comprend le cerveau. Un calcul de distance est alors effectué
entre celles-ci. Deux résultats sont possibles : soit avoir une
image de distances complète, soit une valeur unique symbolisant
l'écart entre les images. De plus, nous souhaiterions être
capables d'obtenir une seule valeur à partir de la carte des distances,
et inversement. La figure 3.1
représente la démarche.
En synthèse d'image, le calcul peut s'effectuer soit dans la
scène, soit sur l'image affichée sur l'écran comme
en analyse. Dans la seconde hypothèse, on rajoutera un dispositif
permettant de connaître l'image affichée en fonction des caractéristiques
précises du moniteur utilisé.

Figure 3.1 : Modèle de vision
Beaucoup de solutions ont été proposées. La plupart
ne prennent en compte que quelques phénomènes. C'est le cas
de [10] ou encore [34].
Cependant, deux modèles sont plus complets. Ce sont les modèles
de Sarnoff [15] et de Daly [7].
3.1 Le modèle de Sarnoff, un algorithme séquentiel
Ce modèle, défini au centre de recherche David Sarnoff, tente
de prendre en compte les phénomènes se produisant dans le
système visuel humain, de manière
séquentielle.
Toutefois, il est important de préciser que ce modèle est
défini pour des images mono-chromatiques. Nous verrons plus loin
que Meyer et Bolin ont proposé, dans [21],
une évolution pour traiter la couleur. Mais, ce n'est pas sans difficultés.
Chaque étape repose sur des mécanismes physiologiques,
permettant ainsi des résultats plausibles. La figure 3.2
représente l'architecture du modèle.

Figure 3.2 : Modèle de Sarnoff
Stimuli
Il s'agit des images de départ, en luminosité.
Système optique
Le but de cette étape est de modéliser la cornée et
le cristallin. On veut prendre en compte l'influence d'un point lumineux
sur la vision des ses voisins. Ceci se fait par une fonction approximant
le phénomène de cercle de confusion. Cette fonction, donnée
par Weistheimer dans [35],
est :
| Q(r)=0,952e |
|
+0,048e |
|
, (3.1) |
avec Q(r) l'intensité lumineuse
en fonction de la distance r à un point
de puissance unitaire.
Échantillonnage
Après avoir obtenu l'image déformée par le système
optique, il faut calculer l'image telle que la voit la rétine. La
méthode choisie est aussi une convolution, mais par une gaussienne.
Le poids affecté dépend de la région. Pour la fovea,
la densité est de 120 pixels par degré. En dehors de la fovea,
la densité décroît suivant l'excentricité.
Malheureusement, Lubin ne donne pas de justification pour le choix des
densités.
Réponse de l'oeil aux bandes passantes de contraste
Les intensités sont converties en contraste local. Lubin propose
d'utiliser, pour cela, une pyramide laplacienne. On obtient ainsi 7 niveaux
de fréquences allant de 0,5 à 32 cycles par degré.
La localité est obtenue en divisant par la valeur de la gaussienne
située deux niveaux plus bas dans la pyramide. Le contraste local
ck(x)
peut se formuler ainsi :
| ck(x)= |
| I(x)*(Gk(x)-Gk+1(x)) |
|
| I(x)* Gk+2(x) |
|
, (3.3) |
avec x un point de l'image, I(x) l'intensité
lumineuse après l'opération Échantillonnage,
et Gk un noyau gaussien tel que
:
| Gk(x)= |
|
e |
|
et sk=2k-1s0.
(3.4) |
Ce type de calcul est assez lourd. L'utilisation d'une transformation en
ondelettes permet un gain en temps significatif pour une précision
similaire (cf 3.1.1).
Réponse orientée
Il s'agit maintenant de tenir compte de l'orientation dans l'image. Pour
cela, Lubin calcule le contraste local donné plus haut suivant quatre
directions : 0, 45, 90 et 135 degrés. Il semble que cela soit un
bon compromis entre précision et temps de calcul. Pour chaque direction,
on a un couple d'opérateurs : la dérivée seconde d'une
gaussienne orientée d'abord, et sa transformée de Hilbert
ensuite. La réponse énergétique en fonction d'une
certaine fréquence et d'une orientation est alors obtenue par la
formule suivante :
| e |
|
(x |
)=(o |
|
(x |
))2+(h |
|
(x))2,
(3.5) |
où o est l'opérateur orienté et h, sa
transformée de Hilbert. L'intérêt d'avoir un couple
de filtres est d'être moins sensible à la position exacte
des zones à forts gradients. En effet, la détection de ces
zones par l'oeil n'est pas au pixel près.
Transduceur
C'est l'opération correspondant au phénomène dit de
transduction visuelle (cf 2.4.4).
De plus, on peut interpréter cela comme le seuil du contraste nécessaire
à la détection.
Étalement
Le résultat, fonction du nombre de cycles, est sensible jusqu'à
un cycle par degré. Or, dans la fovea, la sensibilité
maximale est à cinq cycles par degré. La solution proposée
consiste à convoluer avec un disque de diamètre 5.
Distance
A ce stade de l'algorithme, on a quatre pyramides de sept niveaux chacune,
donnant le contraste dans l'image de départ en fonction des phénomènes
psycho-visuels entrant en jeu. Il s'agit donc de comparer les résultats
obtenus pour les deux images.
D'abord, les premiers niveaux de la pyramide sont ``étirés''
pour avoir la même taille que le niveau le plus bas. On obtient alors
un vecteur de dimension 28 pour chaque pixel. Ensuite, on calcule la distance,
dans l'espace LQ, entre les pixels
des deux images, ce qui nous donne une
image de distances.
| D(x1,x2)
= |
{ |
|
|
[ |
Pi(x1)
- Pi(x2) |
] |
|
} |
|
(3.6) |
Q prend généralement comme valeur 2,4. Lubin ne donne
pas d'explications à cela. Cependant, 2,4 est une valeur aussi utilisée
dans d'autres modèles.
Outre la carte de distances, une valeur unique peut-être générée.
Cela permet d'avoir un descripteur de qualité d'images, et de comparer
voire même de classer plusieurs images.
3.1.1 Améliorations
En synthèse d'images, le principal reproche que nous pouvons faire
à ce modèle, est son approche mono-chromatique. Meyer et
Bolin ont proposé, lors du
SIGGRAPH 98, une évolution
traitant la couleur [21]. Nous
verrons aussi que les auteurs utilisent une transformée en ondelettes
moins coûteuse que la pyramide laplacienne associée aux filtres
gaussiens.
La première étape, Système optique, du modèle
de Sarnoff est supprimée. A la place, on trouve un passage dans
l'espace colorimétrique SML. L'étape Échantillonnage
est aussi abandonnée.
Le contraste en fonction d'une bande de fréquence et d'une orientation
est calculé à l'aide d'une seule transformation : les
ondelettes de Haar. Pour une bande de fréquence, trois types
de contrastes sont détectés : horizontalement, verticalement
et obliques. Cette dernière classe regroupe aussi bien les orientations
à 45qu'à 135. Le schéma
3.1
illustre cette répartition.
| d3 |
d2 |
d3 |
| d1 |
c |
d1 |
| d3 |
d2 |
d3 |
Table 3.1 : Prise en compte des orientations avec les ondelettes de
Haar.
|
|
= |
|
|
(cl[x,y]
+ cl[x,y+1] + cl[x+1,y]
+ cl[x+1,y+1]) |
|
(3.7) |
|
|
= |
|
|
(cl[x,y]
- cl[x,y+1] + cl[x+1,y]
- cl[x+1,y+1]) |
|
|
|
|
= |
|
|
(cl[x,y]
+ cl[x,y+1] - cl[x+1,y]
- cl[x+1,y+1]) |
|
|
|
|
= |
|
|
(cl[x,y]
- cl[x,y+1] - cl[x+1,y]
+ cl[x+1,y+1]) |
|
|
La grosse différence avec le modèle de Sarnoff tient dans
la gestion de la couleur. Meyer et Bolin proposent de passer dans l'espace
AC1C2.
Cela permet de prendre en compte l'aberration chromatique. Ainsi, sur le
canal achromatique, la fonction CSF est celle donnée par
Barten dans [4] et [5].
Sur les canaux en opposition rouge/vert et bleu/jaune, elle est construite
à partir des données fournies par Mullen [22].
Ce sont les principales différences apportées par Meyer
et Bolin. L'architecture du modèle reste la même. Ainsi, une
image de distances ou une valeur sont calculées à partir
des images correspondant aux différentes sensibilités fréquentielles
et angulaires.
3.2 Le modèle de Daly, Visual Difference Predictor
Quoique destinée à prédire la qualité des images,
l'approche proposée par Daly est assez différente. Elle s'appuit
sur la physiologie mais n'est pas optimisée en temps. De plus, le
calcul se fait sur l'image affichée. C'est à dire en fonction
d'une certaine distance à l'écran. Ce modèle, également
séquentiel, est structuré en trois étapes (figure
3.3)
:
-
la non linéarité de la réponse,
-
l'utilisation d'une fonction de sensibilité au contraste
(CSF) pour détecter les fréquences spatiales et les orientations,
-
la prise en compte des mécanismes : masquage et fonction
psychométrique.

Figure 3.3 : Modèle de Daly
3.2.1 Amplitude non linéaire
On ne travaille qu'en luminosité. Daly propose de modéliser
la réponse rétinienne par l'équation suivante :
R/Rmax est la réponse
normalisée en fonction de la luminosité L. Cette phase
simulant la transduction visuelle est assez approximative. Daly ne donne
pas de justifications quant à la valeur des constantes. La fonction
sigmoïde utilisée dans le modèle de Sarnoff est plus
proche des résultats obtenus par Bader dans [2].
D'autre part, nous pouvons de suite remarquer que le modèle n'intègre
pas le système optique de l'oeil. Ce phénomène pourtant
indispensable peut être facilement rajouté en pré-traitement,
grâce à une convolution gaussienne par exemple.
3.2.2 Fonction de sensibilité au contraste
Nous avons vu en 2.4.6
que nous sommes moins sensibles aux détails dans les zones à
hautes fréquences. Pour chaque fréquence, il y a donc un
contraste seuil au dessus duquel nous ne détectons rien. La fonction
utilisée est en deux dimensions, ce qui permet de prendre en compte
à la fois les fréquences et les orientations.

Figure 3.4 : Fonction CSF en deux dimensions
Nous pouvons remarquer sur la courbe que la sensibilité à
45est bien inférieure à celles pour les directions horizontale
ou verticale.
3.2.3 Mécanismes de détection
A partir de là, plusieurs phénomènes sont gérés.
Premièrement, les fréquences spatiales sont repérées.
Ensuite, le masquage est intégré au modèle. Troisièmement,
Daly propose l'utilisation d'une fonction psychométrique modélisant
la probabilité de détection du contraste. Enfin, ces résultats
doivent être combinés, donnant ainsi une idée de la
réponse perceptuelle en chaque pixel.
Fréquences spatiales
Le contraste en fonction d'une plage de fréquence et d'une orientation
est calculé grâce à une transformation nommée
Cortex
Transform, définie par Watson dans [33].
Elle se compose de deux filtres, l'un fréquentiel, dom filter,
l'autre angulaire, fan filter.
-
Dom filter :
| m0(u,v)
= ( |
|
)2 e |
|
*P( |
|
) (3.9) |
mk(u,v) =
m0(2ku,
2kv) (3.10)

Figure 3.5 : Filtre fréquentiel
Un premier filtre correspondant à une plage [0;k] est d'abord
calculé. La composante radiale est non linéaire. Ensuite,
il suffit de faire la différence avec son suivant pour obtenir la
sensibilité sur une plage [k;k+1] (cf. figure 3.6).
dk(u,v) =
mk(u,v)
- mk+1(u,v)
(3.11)

Figure 3.6 : Filtre fréquentiel relatif
-
Fan filter : Soit N, le nombre de filtres1.
L'écart angulaire de chaque filtre est donc de : theta0=180/N.
Le filtre f peut alors se calculer suivant la formule suivante
:
| fanf(theta) |
| = |
|
{1+cos[ |
| Pi*|theta-thetacf| |
|
| theta0 |
|
]},
pour |theta-thetacf|
<= theta0 |
|
| = 0, pour |theta-thetacf|
> theta0, |
|
avec thetacf, l'orientation du sommet du filtre f,
soit thetacf = (f-1)theta0
- 90.
La figure 3.7 représente
la projection sur un plan du filtre angulaire ainsi calculé.

Figure 3.7 : Filtre angulaire
Le filtre final n'est alors que la composition de ces deux opérateurs
(figure 3.8) :
Cortexk,l(r,q)
= Domk(r)
·Fanf(q).
(3.12)
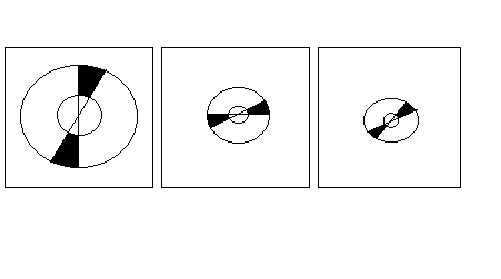
Figure 3.8 : Filtre cortical
Fonction de masquage
Daly définit l'information de masquage comme le produit de la fonction
CSF
par l'opérateur Cortex appliqué à l'image.
m(r,q)
= I * csf(r,q)
* cortex(r,q)
(3.13)
L'auteur introduit ensuite d'autres notions que nous ne détaillerons
pas. Il s'agit de la modification du masquage suivant la phase et de l'effet
d'apprentissage.
Fonction psychométrique
Le caractère aléatoire est enfin modélisé par
la fonction psychométrique.
3.3 D'autres approches
3.3.1 Distance perceptuelle à base d'ondelettes
Gaddipatti et al. ont défini une distance perceptuelle entre images
[10]. Elle repose sur la
combinaison d'une transformation en ondelettes, celles de Daubechies
en l'occurence, avec la fonction
CSF en deux dimensions.
Soit W(m,x), le résultat de la transformation
en ondelettes au niveau
m au pixel x.
Il faut d'abord établir une pondération sur chaque niveau.
Ce poids représente le volume sous la surface CSF, pour une
bande de fréquence (BF) donnée. Pour p,
la fréquence maximale, on a :
| Cm= |
|
, avec BFm
= |
( |
|
, |
|
) |
. (3.15) |
On définit alors la sensibilité S au niveau
m
en x comme :
S(m,x) = CmW(m,x).
(3.16)
La métrique perceptuelle n'est autre qu'une moyenne des différences
de sensibilité.
3.3.2 Un tracé de rayons fréquentiel
Gary Meyer et Mark Bolin ont aussi proposé un algorithme de tracé
de rayons en fonction des fréquences spatiales [20].
Il est basé sur la méthode de compression JPEG.
Le domaine est divisé en blocs de taille 8 par 8 pixels. L'idée
principale est de trouver la représentation fréquentielle
sur chaque bloc. Ceux-ci sont alors triés selon leur importance
en fonction de la CSF. A un instant t, on tire des échantillons
dans les blocs significatifs. En réitérant le processus,
on obtient une image calculée selon les bonnes fréquences.
De plus amples explications peuvent être trouvées dans
[20].
3.3.3 Le modèle de Watson
Nous parlerons, enfin, du modèle de vision défini par A.
Watson et J. Solomon [34].
Très similaire au modèle de Sarnoff, nous retrouvons
la même organisation séquentielle.

Figure 3.9 : Modèle de Watson
Chaque image, en luminance, subit des transformations successives
; les résultats sont ensuite comparés et sommés.
Remarquons l'absence de pré-traitement par un filtre passe-bas,
simulant le système optique de l'oeil. La première étape
du modèle consiste à récupérer les informations
fréquentielles suivant la fonction de sensibilité au contraste
(CSF) combinée à une transformation de Gabor
[9] [11].
Cette opération est un cas particulier de la transformée
de Fourier fenêtrée, aussi appelée
Short-Time Fourier
Transform.
Celle-ci peut s'écrire :
| Xg(tx,w)
= k |
S |
x(t)g(t-tg)e |
|
dt. (3.18) |
La plupart du temps, la fonction g est de la forme :
|
| g(t) |
=1, t appartient à[t1;t2] |
|
=0, sinon. |
|
On a alors bien la transformée de Fourier réduite à
l'intervalle [t1;t2].
Lorsque g est une fonction gaussienne sur [t1;t2],
on appelle Xg transformation de
Gabor. Il est ainsi possible de connaître les fréquences localement
dans l'image.
Ensuite, les auteurs construisent une pyramide, la taille de chaque
niveau n étant divisée par un facteur 2n.
Comme avec la pyramide laplacienne du modèle de Sarnoff (cf. 3.1),
cette opération permet d'obtenir les composantes fréquentielles
de l'image.
Le signal est divisé en deux parties inhibitrice et excitatrice.
Chacune suit une fonction non linéaire de la forme xp.
Différentes valeurs de p sont admises. Les auteurs se conforment
au modèle de Teo et Heeger [30]
[31] où p est égal
à 2. De plus, le signal inhibiteur est convolué par un filtre
gaussien. Il ne reste plus qu'à réunir les deux signaux pour
obtenir le contraste relatif pour chaque image.
La distance finale est calculée dans l'espace L4.
-
1
-
Daly choisit N=6


















