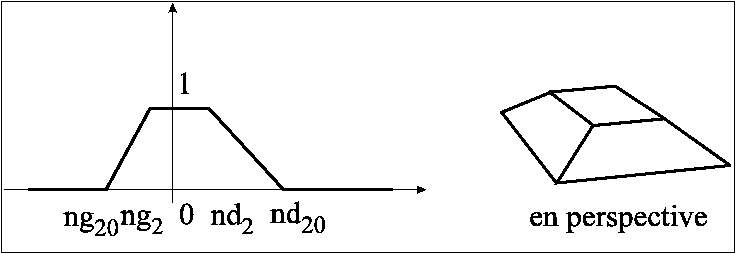Chapitre 1 : Travaux préliminaires

La définition d'une distance entre images est un problème fondamental. Si, en traitement et analyse d'images, des travaux ont été effectués, peu de résultats en revanche sont connus pour la synthèse d'images. Or, le problème est tout aussi crucial. De plus, quel que soit le domaine d'application, cette voie de recherche n'en est qu'à ses débuts.

Nous allons maintenant présenter les solutions proposées par Gilles Rougeron dans [28], sur lesquelles nous nous sommes appuyés.

1.1 Cadre d'étude

La particularité de la distance présentée est d'être spécifique à la synthèse d'images. L'auteur a choisi d'utiliser tous les avantages que procure la synthèse d'images, à savoir :

la parfaite connaissance de la géométrie de la scène ;
la possibilité de travailler avec des grandeurs physiques.

D'autre part, il faut noter que l'espace colorimétrique LLAB, décrit en 1.3, est utilisé.

La méthode suppose plusieurs hypothèses :

Le point de vue doit être identique pour les deux images ;
les objets de la scène ne doivent pas comporter de textures ;
la scène ne doit contenir qu'un seul type de source lumineuse.

Ces restrictions réduisent beaucoup le champ d'application de la distance. Nous verrons, plus loin, que nous pouvons nous en passer.

1.2 Champs visuels

L'auteur propose de prendre en compte l'acuité visuelle de l'observateur. Ainsi, à chaque pixel, on associe deux masques représentant les champs visuels de 2 et 20 degrés. Cela correspond à la zone fovéale¹ et à la zone d'arrière-fond.

La figure 1.1, tirée de [28], représente les masques associés à chaque pixel.

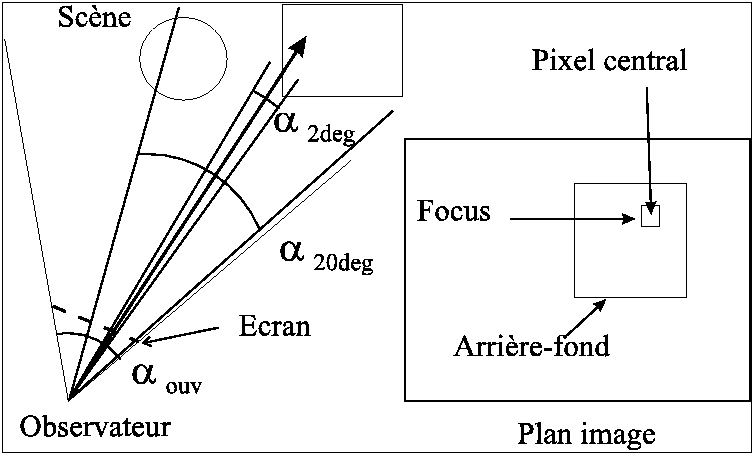
Figure 1.1 : Champs visuels associés à chaque pixel.

D'autre part, l'acuité visuelle étant meilleure dans la zone fovéale, le masque est pondéré avec un poids de 1 pour le focus. La zone d'arrière-fond est pondérée linéairement de manière décroissante de 1 à 0, du centre vers les bords.
La figure 1.2 illustre cette distribution.

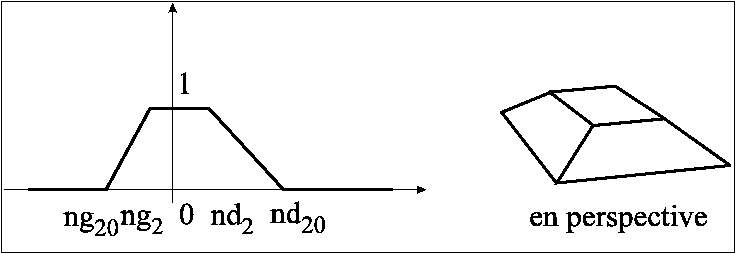
Figure 1.2 : Distribution des poids dans le champ visuel.

L'espace LLAB impose que la cible soit uniforme. Or, la portion d'image dans la zone fovéale peut contenir plusieurs objets. Connaissant facilement la géométrie de la scène, une segmentation est effectuée pour ne garder que les pixels appartenant à la même face du même objet que le pixel central (cf. figure 1.3). Le reste de la zone de focus est considéré comme appartenant l'arrière-fond.

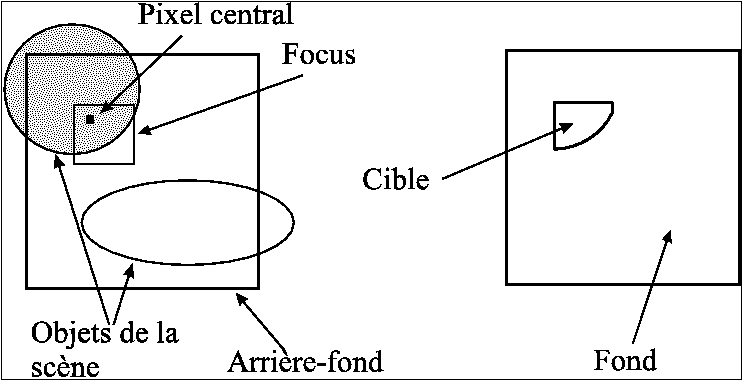
Figure 1.3 : Segmentation du champ visuel.

1.3 L'espace colorimétrique LLAB

Ces dernières années, de nombreux travaux sur la couleur ont aboutit à des propositions. Les espaces LLAB, défini par Luo dans [16], RLAB [8] et Hunt94 [14], [13] en sont des exemples. Se basant sur l'apparence des couleurs, ils permettent de calculer les différences entre couleurs. Gilles Rougeron a choisi d'utiliser le premier.

Le détail des calculs peut être trouvé dans [28].

La première étape est constituée d'un recalage sur une source lumineuse de type D6500 à partir d'une source quelconque, connaissant ses composantes XYZ. Des transformations matricielles permettent d'obtenir les composantes du pixel sous l'éclairage d'une source D6500.

La seconde étape est inspirée de l'espace CIE Lab 1976. Ainsi, des valeurs de clarté (L_L), opposition rouge-vert (A_L), opposition jaune-bleu (B_L), chromaticité (C_L), angle de teinte (h_L) et teinte (H_L) peuvent être calculées sur la zone de focus. La valeur médiane de chaque canal est alors affectée au pixel central. Les trois canaux utilisés sont L_L, C_L et H_L.

La conversion LAB repose sur des valeurs fixes. Cependant, ce n'est pas le cas ici. Les constantes dépendent de la clarté L_L au pixel courant. Cela nous empêche d'exploiter toute forme de cohérence, et donc oblige à recommencer tous les calculs pour chaque pixel.
Pour une image de dimension 512 par 512, la taille moyenne du masque est de 7,6², soit 57,7 pixels. Pour chaque image, on a donc 512 × 512 × 7,6² = 1,51 × 10⁶ conversions LLAB.

1.4 Calcul de distance

Soit Z_p la zone de focus segmentée affectée au pixel p. La conversion de l'espace XYZ vers LLAB peut se formaliser de la façon suivante : LLAB(p) = mediane(F(p)) On note F(p), la fonction calculant les valeurs LLAB en un seul pixel p de la zone de focus. L'écart couleur est ensuite calculé pour tous les pixels des images I₁ et I₂.

Quel que soit p, distance(p) = ABS(LLAB(p

I₁

) - LLAB(p

I₂

)).

1.5 Résultats

Des tests ont été effectués sur la scène standard nommée ``Cornell Box''. Trois algorithmes de rendu différents ont été utilisés :

Tracé de rayons avec terme ambiant ;
Tracé de rayons avec la méthode d'interpolation vectorielle de la composante indirecte [36] (VEI) ;
méthode de Monte-Carlo avec 256 échantillons par hémisphère.

Monte-Carlo Ambiant VEI

14 h 5 mn 13 s 3 mn 27 s 4 mn 9 s

Distance moyenne 12,24 4,17

Table 1.1 : Cornell Box : Résultats des tests.

Sur une station Silicon Graphics Indigo 2, équipée d'un microprocesseur R10000 cadencé à 250 Mhz, le temps de calcul est d'environ 32 minutes.

1.6 LLAB est-il bien approprié ?

Après avoir discuté de l'intérêt d'LLAB, nous évoquerons quelques espaces fréquemment utilisés, parmi lesquels LAB, qui nous semble être la meilleure solution.

Si les résultats avec LLAB sont qualitativement encourageants, il n'est évidemment pas envisageable d'utiliser cela dans un algorithme de tracé de rayons. Les temps de calcul sont beaucoup trop importants du fait de l'emploi de LLAB.

Il convient donc de se demander si cet espace couleur est bien utile.
Nous pouvons déjà remarquer que l'auteur ne l'exploite pas dans les conditions strictes où il a été défini. En effet, Luo, dans [16], impose que la cible soit uniforme et le fond achromatique. Cette seconde condition n'est pas remplie. Il nous est alors difficile de garantir la validité de LLAB.

Ensuite, Gilles Rougeron impose, à notre sens, beaucoup trop de contraintes. Les scènes que nous souhaitons synthétiser comportent souvent plusieurs sources lumineuses, de plus différentes. Ceci est encore en contradiction avec la définition de LLAB. Enfin, les textures ne peuvent pas être prises en compte.

Avec un champ d'application réduit, des temps de calcul prohibitifs, nous estimons que cet espace colorimétrique n'est pas utilisable à l'heure actuelle.

1.6.1 Les espaces basiques

Nous ne nous étendrons pas sur la description de ces espaces. Citons les plus répandus : RVB et XYZ. Ces espaces ne sont pas uniformes. On ne peut donc garantir la véracité des distances calculées. C'est pour cela que la Commission Internationale de l'Eclairage, CIE, tente de définir de meilleures solutions.

1.6.2 L'espace CIECAM97

C'est à partir des trois modèles LLAB, Hunt et RLAB que Luo et Hunt ont proposé, dans [17], un nouvel espace, CIECAM97, tentant de prendre les avantages de chacun. Il repose sur trois étapes :

une transformation d'adaptation chromatique. C'est la phase de recalage sur un blanc de référence. La transformation utilisée est celle de Bradford.
une fonction de réponse dynamique. Cette fonction modélise la réponse minimale de 1 pour les faibles stimulus et maximale de 41 pour les stimulus importants. La transition entre les deux approxime une fonction racine.
une projection dans un espace couleur pour représenter les données.

On obtient alors un espace à 7 dimensions représentant : l'angle de teinte, la teinte, la luminosité, le contraste, la saturation, la chromaticité et le piqué des couleurs.

Nous ne donnerons pas le détail des opérations qui peuvent être trouvées dans [17].

Si cet espace semble, a priori, donner de meilleurs résultats que LLAB, il ne permet toujours pas l'emploi de sources lumineuses diverses dans une même scène. De plus, les temps occasionnés risquent d'être, là encore, prohibitifs.

1.6.3 L'espace LAB

Cet espace présente le double avantage d'être uniforme (pour les petites valeurs), tout en restant plus facilement calculable. S'il n'y a pas de solution miracle, celle-ci nous semble être la moins pire comparativement aux espaces présentés ci-avant.

1: aussi appelée zone de focus.


Monte-Carlo	Ambiant	VEI
14 h 5 mn 13 s	3 mn 27 s	4 mn 9 s


Distance moyenne	12,24	4,17